Welcome toMichael Psenka

The centralized location for everything Michael Psenka that no one asked for.

Download Curriculum Vitae

About

Research

Industry & Projects

Extras

About Me

I use geometry to build general-purpose deep learning models that build themselves.

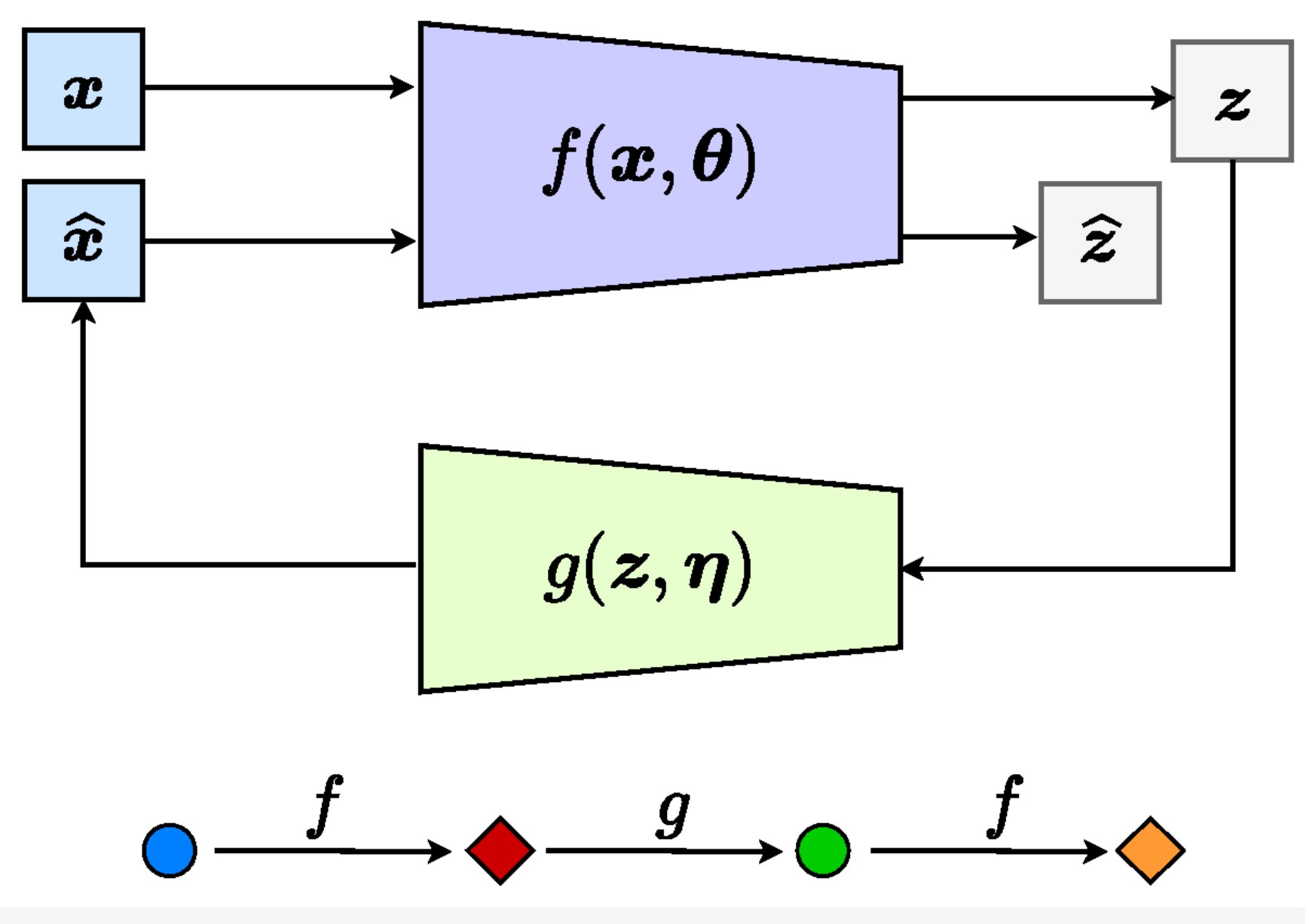
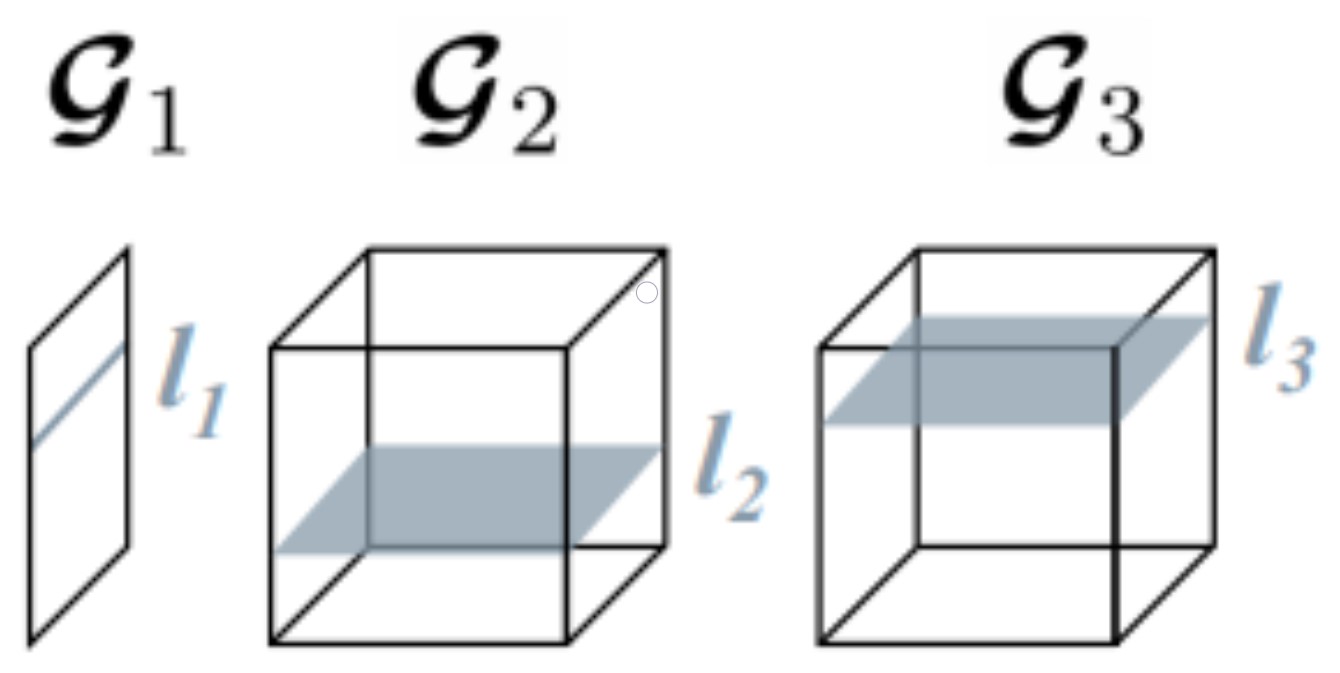
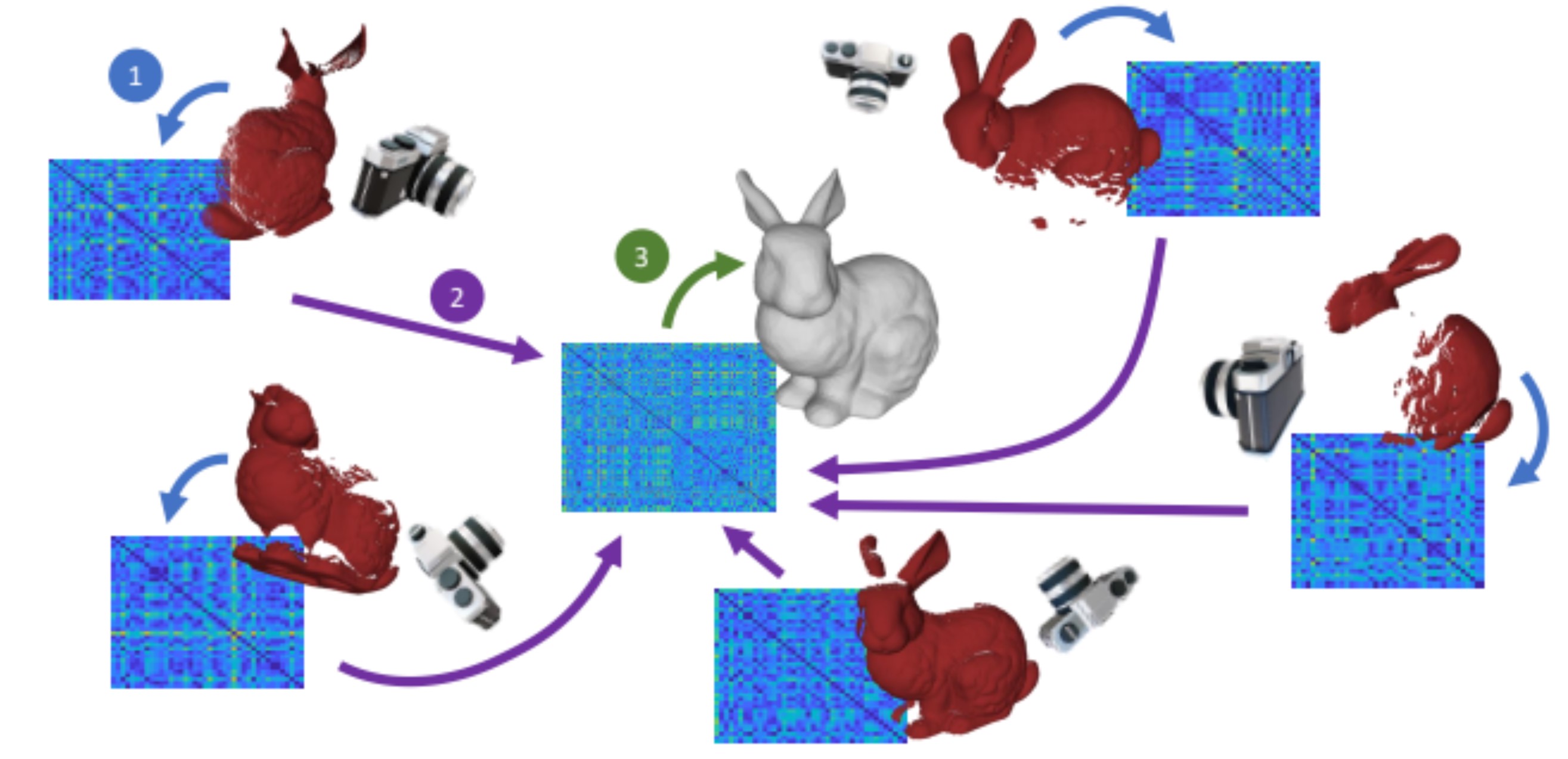
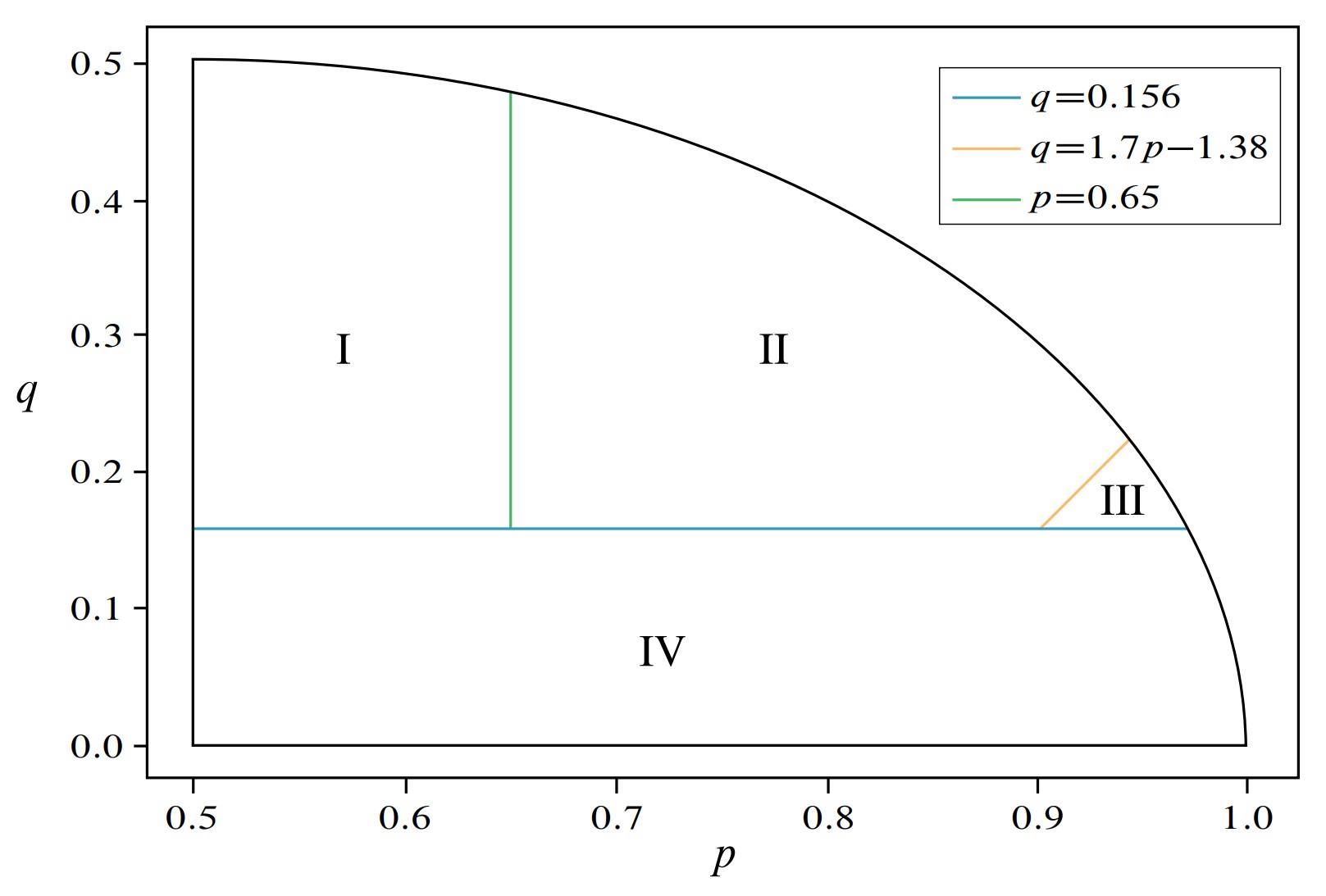
I am a second-year PhD student in Electrical Engineering and Computer Science at UC Berkeley, advised by Prof. Yi Ma. With my math background, I break down modern deep learning systems to their core components, yielding interpretable models that are just as powerful.

The easier the model is to work with and deploy, the happier I am.

Education

Sample Image

University of California, Berkeley | MS/PhD in EECS

Focus in AI. GPA: 4.0.

2021-2026
Sample Image

Princeton University | A.B. in Mathematics

Certificates (minors) in CS and Applied Math. GPA: 3.6. Involvements: Princeton Pianist Ensemble, Math Club, Princeton Data Science, Princeton ACM, HackPrinceton participant.

2017 - 2021

Awards

Sample Image

Peter A. Greenberg '77 Memorial Prize for Mathematics

June 2020

Awarded for solving an open problem in spectral geometry with three classmates.

"Awarded for outstanding accomplishments in Mathematics by juniors".
Sample Image

Manfred Pyka Memorial Prize for Physics

June 2018

Performed exceptionally well in an experimental first-year physics-major sequence, which introduced modern topics very quickly.

"Given to outstanding Physics undergraduates who have shown excellence in course work and promise in independent research".
Sample Image

First Place, HackPrinceton

April 2018

Won first place for A.I.D.A.N., a chatbot that allows you to interact with your data via advanced statistical and machine learning tools.

Best overall project at the HackPrinceton hackathon.

I focus on: AI.

...

Publications & Workshop Presentations

Sample Image
Representation Learning via Manifold Flattening and Reconstruction.
Michael Psenka, Druv Pai, Vishal Raman, Shankar Sastry, Yi Ma.
Submitted to JMLR, May 2023.
Paper Code
Sample Image
Pursuit of a discriminative representation for multiple subspaces via sequential games.
Druv Pai, Michael Psenka, Chih-Yuan Chiu, Manxi Wu, Edgar Dobriban, Yi Ma.
Journal of the Franklin Institute, April 2023.
Paper Code
Sample Image
CTRL: Closed-Loop Transcription to an LDR via Minimaxing Rate Reduction
Xili Dai, Shengbang Tong, Mingyang Li, Ziyang Wu, Michael Psenka, Kwan Ho Ryan Chan, Pengyuan Zhai, Yaodong Yu, Xiaojun Yuan, Heung Yeung Shum, Yi Ma.
Entropy Journal, March 2022.
Paper Code
Sample Image
Second-order optimization for tensors with fixed tensor-train rank.
Michael Psenka, Nicolas Boumal.
NeurIPS OPT 2020.
Paper Code
Sample Image
Reconstruction Without Registration.
Michael Psenka, Tolga Birdal, Leonidas Guibas.
IROS 2020 geometric methods workshop.
Paper Code
Sample Image
A Proof of The Triangular Ashbaugh-Benguria-Payne-Pólya-Weinberger Inequality.
Ryan Arbon*, Mohammed Mannan*, Michael Psenka*, Seyoon Ragavan*.
Journal of Spectral Theory, Sept. 2022.
Paper

Employment

Sample Image

Co-Head Instructor @ UC Berkeley

Jun - Aug, 2022
  • Organized and taught lectures for CS 70, an undergraduate class for discrete math and probability theory.
  • Link to class page.
Sample Image

Undergrad Researcher @ Stanford University

Jun - Aug, 2020
  • Worked with Dr. Tolga Birdal on a novel approach to multi-view reconstruction in computer vision that bypasses pairwise view registration.
Sample Image

Undergrad Researcher @ Princeton University

Jun - Sept, 2019
  • Successfully developed a state-of-the-art method for computing analytic Hessians and second order optimization over tensor train manifolds.
  • Undergraduate research funded by the National Science Foundation through award DMS-1719558.
Sample Image

Software Developer @ Moovila

June - Aug 2018, '17, '16
  • Developed a machine learning algorithm for workplace analytics.
  • Mathematically modeled collision avoidance in network analysis animation.
  • Worked through a patent application for proprietary software.
  • Worked on improving the search engine for quicker and more robust search results.
  • Denormalized relational database to NoSQL, maximizing data access efficiency and cost-efficiency

Projects

Sample Image

my VS Code extension

Bookmarks Table of Contents Generator
Sample Image

my academic PDF tool

citelink
  • Changes all bibliographic links in an academic PDF into direct URL's straight to the paper.
  • Saves a lot of time for related work reading of papers.
  • Link to Github repo.
Sample Image

pip package for manifold linearization

flatnet
  • Easy to use package for automatically building neural networks that flatten data manifolds.
  • Built from research on this paper.
  • Link to repo.
Sample Image

some UI/UX tools

michaelpsenka.io
  • The stuff I wrote for this website! If you like anything here, you may find it in this project.
  • Link to repo.

My Music

I'm a classically trained pianist with some experience playing jazz. Recently, I started tinkering around with making music in a digital workstation. Here, I'll upload anything that becomes a finished product.

I'm also a member of the Princeton Pianist Ensemble! My most recent performance was a duet version of Fly Me To The Moon for a virtual concert: Link to video. You can find more from the ensemble here.

1. Hurricane

Drum sample: Incredible Bongo Band - Apache

2. Deadly

Drum sample: Kanye West - Black Skinhead
Close